Particle Based Samplers for MCMC
Chapter 1 Introduction to particle based sampler for MCMC
Contains implementations of particle based sampling methods for model parameter estimation. Primarily an implementation of the Particle Metropolis within Gibbs sampler outlined in the paper available here, it also contains code for covariance estimation.
1.1 Assumed knowledge
To get the most out of this tutorial for the PMwG sampler, we assume you are familiar with hierarchical Bayesian estimation and MCMC sampling. If you would like to read more on these topics, please see Shiffrin et al. (2008) tutorial on Hierachical Bayesian Methods and Van Ravenzwaaij, Cassey, and Brown (2018) introduction to Markov Chain Monte-Carlo Sampling.
1.2 Why would you use Particle Metropolis within Gibbs sampling?
This software is intended to help estimate models in a hierarchical structure with random effects for subjects. You will need to be able to write a function that evaluates the density of one subject’s data, given values for that subject’s parameters (i.e. their random effects). Everything else is taken care of by the sampler functions. The model that defines the density for an individual subject’s data could be a regression model, a simple cognitive model like signal detection models (which is one of the examples we cover here), or models that can be very challenging to estimate, such as the Linear Ballistic Accumulator (LBA) or the Drift Diffusion model. As long as you have a model for which you can provide a likelihood, the PMwG software will help estimate the model in a hierarchical Bayesian way.
Benefits of the Particle Metropolis within Gibbs sampling algorithm include:
It allows you to efficiently get posterior samples from difficult-to-estimate models with highly correlated parameters, such as the LBA or diffusion model, and these samples have nice properties (e.g., lower autocorrelation than other MCMC samplers).
Statistical efficiency makes it feasible to draw a large number of posterior samples. This can be important in posterior inference, for example in calculating Bayes Factors using established methods.
It allows you to estimate the covariance structure between parameters in a principled manner.
1.3 The assumed hierarchical structure
The PMwG package is very flexible in that it is agnostic about the data-level model; it allows the user to specify the model that defines the density of each subject’s data. However, the package makes fixed assumptions about the hierarchical structure across participants. The package assumes a multivariate normal random effect structure. For example, when estimating an LBA model, each participant will have several parameters, such as a start point (A), threshold (b), drift rate (v), and non-decision time (t0). The PMwG package assumes that the vector of each subject’s parameter value follows a group-level distribution which is multivariate normal. The algorithm will estimate the group-level mean for each parameter, as well as its variance, and also the correlations between parameters in the sample.
One consequence of the multivariate normal assumption is that all parameters are assumed to be unbounded (i.e. able to take values anywhere on the real line). Cognitive models often have bounded parameters (e.g. in the LBA model, the non-decision time parameter cannot be negative, as it represents a length of time). The user should deal with bounded parameters by transforming them to be unbounded. We give examples of that, in the likelihood functions.
1.4 What Particle Metropolis within Gibbs sampling provides
The sampler will provide samples from the posterior distribution of the model in three categories:
The means for the group level parameters (
theta).The vectors of random effects for each subject (individual level parameter values,
alpha)The group-level variance covariance matrix (
sigma).
1.5 What is Particle Metropolis within Gibbs sampling?
There are two sampling approaches incorporated into PMwG. One is the well-established and easy to apply Gibbs sampling on the group-level parameters. Gibbs sampling is very powerful and efficient, and it can work for the group-level parameters because the package assumes a multivariate normal distribution, which is easy to work with.
However, for the subject-level parameters (random effects), Gibbs sampling is not possible; at least not for most cognitive models. For this reason, the PMwG package uses particle methods to sample random effects. Particle sampling works like other Markov chain samplers, such as Metropolis-Hastings. At each step, the sample (the vector of random effects) from the previous step is compared to a large number of proposals (“particles”). The new sample is chosen from amongst the particles (including the previous sample), according to how well they match the data and the prior.
The key to making the algorithm efficient is to propose particles carefully. Our algorithm uses adaptive proposal distributions, individually tuned for each participant, to make sure that good proposal particles are generated without requiring a prohibitively large number of particles in total. How often the sampler accepts a new particle (compared to the previous sample) is referred to as the acceptance rate. Acceptance rate can be adjusted for maximum efficiency (somewhere around 30-50% acceptance is great) by changing the total number of particles and by changing the variance of the proposal distribution (parameter “epsilon”). The particles are evaluated in parallel, which increases computation speed.
1.6 Generating proposals in PMwG sampling using Particle Metropolis
PMwG has three sampling stages (demarcated by the black, vertical lines in the plot below). The first stage is called burn-in, the second is adaptation, and the third is the sampled stage. The stages employ different numbers of particles, and different proposal distributions. This makes the algorithm most efficient.
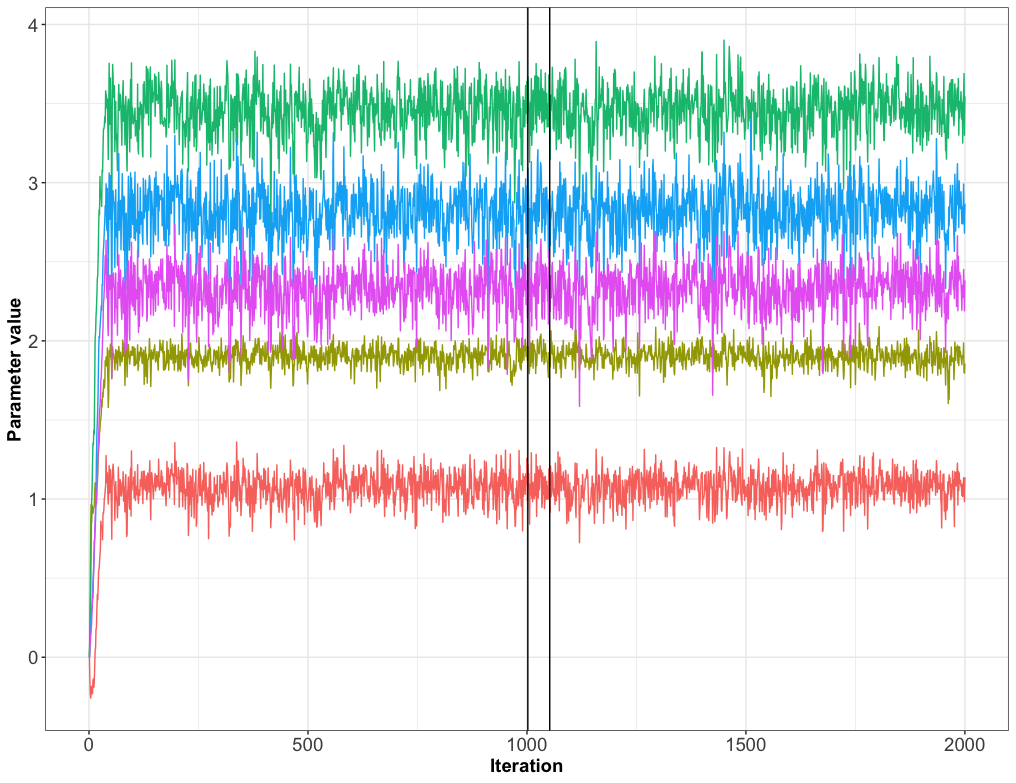
Figure 1.1: Trace plot with vertical lines demarcating the PMwG sampler’s three sampling stages
In the burn-in and adaptation stages, the proposals (or random effects vectors) for each subject are sampled from a mixture of two sources. One source is the group-level distribution and the second source is a multivariate normal distribution centred on the current best guess for the subject’s random effects vector (alpha), with a variance that is smaller than the group level distribution. We generate proposals from both sources, because proposals generated from the group level distribution act as a safety net in situations where proposals generated from the subject’s current alpha are unusual or unlikely. If this occurs instead of the sampler taking a long way to return a sensible vector of random effects, a group level proposal will instead be chosen, leading to a faster sampling time.
One thing we want to know is the posterior distribution for each subject’s random effects (alpha). For this reason, we throw away samples from the burn-in stage, because this is a period in which the sampler is trying to move away from an initial guess, and stabilise on samples which are from the true posterior distribution for each subject’s random effects.
In the adaptation stage, we continue the algorithm used in the burn-in stage until we collect a minimum of 20 unique samples from each subject’s posterior distribution. These samples are used to give a good idea of what the posterior distribution looks like for each subject’s random effects vector. That allows us to build an adaptive proposal distribution that makes very efficient proposals, in the next stage.
In the final sampling stage (sample), we generate a multivariate normal distribution (referred to as the adaptive proposal distribution), that summarises the unique samples in the adaptation stage, and use this to generate future proposals. An important feature of this distribution is that, for each subject, it summarises not only the posterior distribution of their random effects but also the way these random effects relate to the group-level parameter. This allows us to draw conditional proposals; proposals which are both consistent with that subject’s random effects and with the current proposal for the group-level distribution. Because of this, the proposals generated are frequently accepted, so we can lower the number of particles needed in this stage (for example, 20 instead of 200), and still maintain an adequate acceptance rate. Further, we continue to update this proposal distribution throughout the sample stage so we have a more accurate proposal distribution.
As a safety precaution during the sample stage, we also include a few proposal particles from the same algorithm as used in the burn-in stage. This protects against very poor conditional proposal distributions.